Czym zajmuje się trygonometria?
Trygonometria to dział matematyki, który zajmuje się badaniem trójkątów, zwłaszcza trójkątów prostokątnych. Służy do opisywania zależności między bokami i kątami trójkąta.

W skrócie
Proporcje boków w trójkącie prostokątnym. Operujemy na kątach
Kilka podstawowych definicji
Trójkąt prostokątny – trójkąt, który ma TYLKO jeden kąt prosty ($90^{\circ}$).
Przeciwprostokątna – najdłuższy bok w trójkącie prostokątnym, leży naprzeciw kąta prostego ($90^{\circ}$).
Przyprostokątna – każdy z dwóch krótszych boków w trójkącie prostokątnym. Są one przyległe do kąta prostego. Jeden z nich przylega do kąta, który rozpatrujemy, a drugi leży naprzeciw niego.

funckje trygonometryczne jakie poznasz
Na poziomie podstawowym poznajemy trzy funkcje trygonometryczne.
Oto one:
Sinus ($sin$) – stosunek długości przyprostokątnej leżącej naprzeciw kąta do długości przeciwprostokątnej.
$sin(\alpha)=\frac{a}{c}$

Cosinus ($cos$) – stosunek długości przyprostokątnej przylegającej do kąta do długości przeciwprostokątnej.
$cos(\alpha)=\frac{b}{c}$

Tangens ($tan$) – stosunek długości przyprostokątnej leżącej naprzeciw kąta do długości przyprostokątnej przylegającej do kąta.
$tan(\alpha)=\frac{a}{b}$
PST! Jest jeszcze cotanges, ale nie musisz go umieć na maturze podstawowej.
Jakie wartości przyjmują funkcje trygonometryczne w każdej ćwiartce
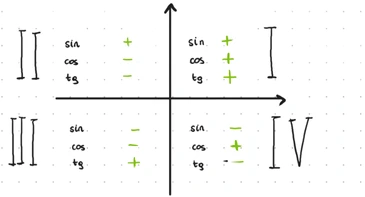
Na maturze podstawowej skupimy się jedynie na pierwszej i drugiej ćwiartce.
Wartości funkcji trygonometrycznych dla wybranych kątów
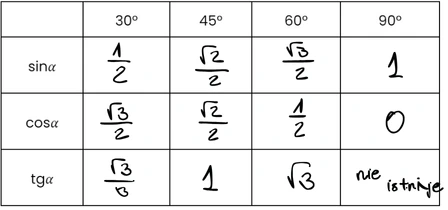

Studencki Tip od Emi
Nie musisz pamiętać tych wartości. Wszystko znajdziesz w tablicach wzorów!
jak wyliczyć sin, cos i tg dla kąta rozwartego
Może się zdarzyć, że zostaniesz poproszony o obliczenie funkcji sinus, cosinus lub tangens dla kąta większego niż $90^{\circ}$. W takim wypadku nie użyjesz wcześniej poznanych wzorów. Z pomocą przychodzi karta z wzorami matematycznymi w dziale trygonometria znajdziesz poniższy rysunek.
$$sin(\alpha)=\frac{y}{r}$$
$$cos(\alpha)=\frac{x}{r}$$
$$tg(\alpha)=\frac{y}{x}, \ \ x\neq0$$
gdzie:
$$r=|OM|=\sqrt{x^2+y^2}>0$$
$|OM|$ to długość odcinka od punkty $O$ do punktu $M$
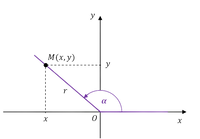
$M$ to punkt o współrzędnych $(x,y)$. Długość odcinka $x$ i $y$, odczytujemy z osi współrzędnych.
Jak obliczyć funkcje za pomocą powyższych wzorów?
Przykład 1. Załóżmy, że nasz punkt $M$ ma współrzędne $(-3, 4)$. Policzmy zatem $sin$, $cos$ i $tg$
1. Liczymy z twierdzenia Pitagorasa długość $r$, czyli długość odcinka $|MO|=|OM|$
$$(-3)^2+4^2=r^2$$ $$9+16=25$$ $$r^2=25$$ $$r=5$$

2. wyznaczamy $x$ i $y$
$$x=-3$$ $$y=4$$
3. obliczamy $sin$, $cos$ i $tg$, czyli teraz tylko podstawiamy do wzorków
$$sin(\alpha)=\frac{y}{r}=\frac{4}{5}$$ $$cos(\alpha)=\frac{x}{r}=-\frac{3}{5}$$ $$tg(\alpha)=\frac{y}{x}=-\frac{4}{3}$$

Studencki Tip od Nati
Tak jak długość odcinka $x$ odczytujemy z osi $X$, tak długość $r=|OM|$ nie możemy odczytać z wykresu lub zmierzyć na oko, trzeba go policzyć. Czemu? Leży on ukośnie względem osi współrzędnych.
Co jeśli nie znamy współrzędnych punktu $M$? Wtedy z pomocą przychodzą poniższe wzory są to tzw. wzory redukcyjne.
$$sin(180^{\circ}-\alpha)=sin(\alpha)$$
$$cos(180^{\circ}-\alpha)=-cos(\alpha)$$
$$tg(180^{\circ}-\alpha)=-tg(\alpha)$$
Przykład 1. Chcemy obliczyć $sin(135^{\circ})$
1. Korzystamy z tego wzoru:
$$sin(180^{\circ}-\alpha)=sin(\alpha)$$
2. Podstawiamy co wiemy:
alfa u nas to $135^{\circ}$
$$sin(180^{\circ}-135^{\circ})=sin(45^{\circ})$$
3. Patrzymy do tabeli i odczytujemy wartość:
$$sin(45^{\circ})=\frac{\sqrt{2}}{2}$$
Przykład 1. Chcemy obliczyć $cos(120^{\circ})$
1. Korzystamy z tego wzoru:
$$cos(180^{\circ}-\alpha)=-cos(\alpha)$$
2. Podstawiamy co wiemy:
Pamiętaj o -. We wzorach redukcyjnych przy cosinusie pojawia się minus
$$cos(180^{\circ}-120^{\circ})=-cos(60^{\circ})$$
3. Patrzymy do tabeli i odczytujemy wartość:
$$-cos(60^{\circ})=-\frac{1}{2}$$
co jest takiego wyjątkowego w tych trójkątach?
Trójkąty o kątach ($45^{\circ}$, $45^{\circ}$, $90^{\circ}$) i ($30^{\circ}$, $60^{\circ}$, $90^{\circ}$) są wyjątkowe, ponieważ ich boki mają stałe, proste proporcje, dzięki czemu łatwo można obliczyć długości boków, znając tylko jeden z nich (w porównaniu w Pitagorasie, potrzebujemy długości dwóch boków). Są to tzw. trójkąty szczególne, często wykorzystywane w zadaniach maturalnych, gdzie szybkie znalezienie proporcji boków jest przydatne.

Jeśli dostaniesz zadanie, gdzie masz daną długość tylko jednego boku to wiedz co tu się święci – właśnie te trójkąty!
trójkąt 45 45 90
Pierwszym z wyjątkowych trójkątów to ten o kątach $45$ $45$ $90$.
Oto jego zależności:

Własności tego trójkąta:
równoramienny, prostokątny, kąty $45$, $45$, $90$
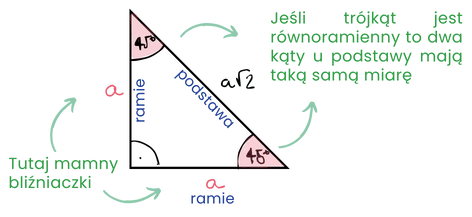
Przykład 1. Wiemy, że trójkąt jest prostokątny, równoramienny. A także, że przeciwprostokątna ma długość $8$. Chcemy obliczyć pozostałe długości boków.


Studencki Tip od Emi
Jeśli zapomnisz tych zależności. Możesz wyliczyć brakujący bok korzystając z twierdzenia pitagorasa.
trójkąt 30 60 90
Drugi wyjątkowy trójkąt jest połową trójkąta równobocznego.
Występują w nim poniższe zależności.

Własności tego trójkąta:
połowa trójkąta równobocznego, prostokątny, kąty $30$, $60$, $90$

Przykład 2. Wiemy, że trójkąt jest prostokąty oraz kąty są w stosunku $1:2:3$. A także, że przeciwprostokątna ma długość $6$. Chcemy obliczyć pozostałe długości boków.


Studencki Tip od Emi
Pamiętaj aby dobrze umiejscowić boki, zwłaszcza kiedy trójkąt będzie odwrócony.
twierdzenie cosinusów - definicja
Twierdzenie cosinusów pozwala nam obliczyć brakujący trzeci bok trójkąta w sytuacji kiedy znamy długości pozostałych dwóch boków oraz miarę kąta między nimi
$$c^2=a^2+b^2-2abcos(\gamma)$$
Przykład 1. Mamy trójkąt $ABC$ $|AB| = 2$ $|AC| = 5$ a cos kąta między nimi wynosi $\frac{3}{5}$. Chcemy obliczyć bok $|BC|$
1. Korzystamy z tego wzoru:
2. Podstawiamy co wiemy:
$$c^2=a^2+b^2-2abcos(\gamma)$$
$$|BC|^2=2^2+5^2+2\cdot 2\cdot 5 \cdot \frac{3}{5}$$
3. Obliczamy:

Studencki Tip od Emi
Wbrew pozorom jest to przydatne twierdzenie zwłaszcza przy zadaniach z działu stereometria
$$|BC|^2=4+25+12$$
$$|BC|^2=41$$
$$|BC|=\sqrt{41}$$
Na pewno znasz ten wzór na pole trójkąta
$P=\frac{1}{2}ah$
Co jeśli nie mamy wysokości lub wszystkich boków trójkąta? Istnieje praktyczny sposób, który umożliwia wyznaczenie pola trójkąta, gdy znamy długości dwóch jego boków oraz kąt między nimi.
Oto on:
$P=\frac{1}{2}absin(\gamma)$
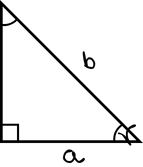
Jak to działa?
Przykład 1. Chcemy obliczyć pole trójkąta $ABC$ wiedząc, że $|AB| = 10$, $|BC| = 12$ a kąt między nimi jest kątem prostym.
1. Korzystamy z tego wzoru:
2. Wyznaczamy $sin(90^{\circ})$
$P=\frac{1}{2}absin(\gamma)$
$$sin(90^{\circ})=1$$
3. Podstawiamy co wiemy i obliczamy:
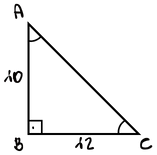
$$P=\frac{1}{2}\cdot 10 \cdot 12 \cdot 1$$
$$P=60$$
