Czym jest niewiadoma?
- Niewiadomą nazywamy coś, czego szukamy w naszym równaniu lub nierówności. Jest jak zamknięte pudełko, którego wartość chcemy poznać
- Skoro nie znamy wartości, trzeba użyć jakiegoś symbolu, aby ją oznaczyć. Z reguły używa się małą literę $x$, ale mogą to być wszystkie litery z alfabetu np. $a$, $b$, $c$, $…$, $y$, $z$
Czym są równania liniowe?
- Równanie liniowe to równanie, w którym niewiadome występują tylko w pierwszej potędze ($x$, $y$, $3x$, $\frac{x}{2}$)
- Dążymy do wyznaczenia wartości niewiadomej x, tak aby po podstawieniu lewa strona równała się prawej (L=P)
Przykład 1. Jak wygląda równanie liniowe?
lewa strona równania
$2$$x$$+3=11$
prawa strona równania

To jak rozwiązać takie równanie i poznać wartość $x$?
Przenieś liczby na jedną stronę
Wszystko, co nie ma przy sobie niewiadomej $x$ wyrzuć na przeciwną stronę
dodawanie, np. $x + 3$
odejmij 3 z obu stron
odejmowanie, np. $x - 3$
dodaj 3 do obu stron
pozbądź się tego, co stoi przy x
Chcemy samego $x$, więc musimy się pozbyć przyklejonej do niego liczby
mnożenie, np. $2x$
podziel obie strony przez 2
dzielenie, np. $\frac {x} {2}$
pomnóż obie strony przez 2
Przykład 2. Rozwiązywanie równania liniowego
Wykorzystajmy poznane wskazówki i rozwiążmy poniższe równanie:
Nasza taktyka: niewiadome na lewą stronę, a liczby znane na prawą. Chcemy samego $x$ z lewej strony. Przeszkadza nam $3$
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $2\fbox{$x$}+3=11$
Aby pozbyć się $3$, musimy obustronnie odjąć $3$
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $2\fbox{$x$}=11-3$
Po lewej mamy $2x$, a chcemy wyliczyć samo $x$
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $2\fbox{$x$}=8$
Przeszkadza nam $2$, zatem dzielimy obustronnie przez $2$
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $\fbox{$x$}=8\div2$
Poznaliśmy naszą niewiadomą! To $4$!:)
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $\fbox{$x$}=4$
Możemy jeszcze sprawdzić, czy po podstawieniu 4 pod x, lewa strona będzie równa prawej:
Przykład 3. Sprawdzenie
$2\cdot$ $4$ $+3=11$
$8+3=11$
$11=11$
$L=P$
Lewa strona $=$ prawa strona, oznacza to, że zadanie jest dobrze rozwiązane!
Definicja dziedziny
- Dziedzina to po prostu zbiór wszystkich wartości, jakie może przyjąć nasza niewiadoma, aby działanie matematyczne dalej miało sens
- Np. nie możemy dzielić przez $0$ w matematyce, więc:
$$\frac {1} {x+2} = 5$$
$x+2$ nie może być równe zero,
więc wykluczamy $x=-2$ z dziedziny

Studencki Tip od Nati
W równaniach liniowych warto robić Sprawdzenie - dobry sposób na wyłapanie błędów. Gdy Lewa strona nie równa się prawej coś jest nie tak!
czym są nierówności liniowe?
Nierówność liniowa to nierówność z niewiadomą w pierwszej potędze, gdzie dążymy do wyznaczenia zakresu (przedziału) wartości tej niewiadomej.
Przykład 1. Jak wygląda nierówność liniowa?
lewa strona nierówności
$2$$x$$+3>11$
prawa strona nierówności

może być też znak $<$ lub $\leq$, $\geq$
To jak rozwiązać taką nierówność i poznać wartość $x$?
Na szczęście bardzo podobnie do równań!
Przykład 2. Rozwiązywanie nierówności liniowej
Nasza taktyka: niewiadome na lewą stronę, a liczby znane na prawą. Chcemy samego $x$ z lewej strony. Przeszkadza nam $3$
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $2\fbox{$x$}+3>11$
Aby pozbyć się $3$, musimy obustronnie odjąć $3$
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $2\fbox{$x$}>11-3$
Po lewej mamy $2x$, a chcemy wyliczyć samo $x$
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $2\fbox{$x$}>8$
Przeszkadza nam $2$, zatem dzielimy obustronnie przez $2$. Liczba jest dodatnia, więc nie zmieniamy znaku.
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $\fbox{$x$}>8\div2$
Poznaliśmy naszą niewiadomą! Czytamy to jako “$x$ jest większe od $4$”
$\renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}}$ $\fbox{$x$}>4$
Odpowiedź możemy zapisać też na drugi sposób. Czytamy ten zapis “$x$ należy do przedziału od $4$ otwarte do plus nieskończoności”
$x \in (4, \infty)$
Możemy jeszcze sprawdzić, czy po podstawieniu czegoś większego od 4 pod $x$, lewa strona będzie większa od prawej
Przykład 3. Sprawdzenie
$2\cdot$ $5$ $+3>11$
$10+3>11$
$13>11$
$L>P$
Lewa strona $>$ prawa strona, oznacza to, że zadanie jest dobrze rozwiązane!
Przenieś liczby na jedną stronę
Wszystko, co nie ma przy sobie niewiadomej $x$ wyrzuć na przeciwną stronę
dodawanie, np. $x + 3$
odejmij 3 z obu stron
odejmowanie, np. $x - 3$
dodaj 3 do obu stron
pozbądź się tego, co stoi przy x
Chcemy samego $x$, więc musimy się pozbyć przyklejonej do niego liczby
mnożenie, np. $2x$
podziel obie strony przez 2
dzielenie, np. $\frac {x} {2}$
pomnóż obie strony przez 2
uwaga!
Jeżeli mnożymy lub dzielimy przez liczbę ujemną (np. $-2$, $-1$) to musimy zmienić (odwrócić) znak nierówności!
$-2x<8$ / :$(-2)$
$-2x>8$ / :$(-2)$
$x>-4$
$x<-4$
czym jest układ równań?
- Układ równań to zbiór dwóch lub więcej równań, które mają wspólne niewiadome (czyli $x$, $y$, $z$, itd.).
- Chcemy w nim poznać wartości więcej niż jednej litery.
czym jest układ równań?
Istnieją na to różne metody. Warto popatrzeć chwilę na przykład i zastanowić się, która w tym przypadku będzie najlepsza do użycia
metoda podstawiania
Metoda podstawiania polega na wyznaczeniu specjalnego wzoru na dowolną niewiadomą z jednego równania (np. $y=2x+5$) i podstawieniu tej wartości do drugiego równania (wszędzie, gdzie jest $y$ wpisujemy $2x+5$).
metoda przeciwnych współczynników
- Metoda przeciwnych współczynników polega na dodaniu lub odjęciu równań tak, aby jedna zmienna nam się zredukowała.
- Żeby to zrobić, musimy stworzyć niewiadome o przeciwnych współczynnikach (to co stoi przy $x$ i $y$). Np. $2x$ i $-2x$, $y$ i $-y$.
- Następnie podstawiamy uzyskaną wartość do jednego z równań, aby znaleźć drugą niewiadomą.
metoda graficzna
Metoda graficzna polega na narysowaniu obu równań w układzie współrzędnych (są to proste, jak funkcja liniowa) i znalezieniu ich punktu przecięcia – jest on rozwiązaniem układu równań.

Studencki Tip od Nati
Metoda graficzna jest fajna, ale raczej rzadko będziemy z niej korzystać. Warto wiedzieć, że istnieje, ale są szybsze sposoby na rozwiązanie układu równań - np. I i II 🙂
Przykład 1. Jak wygląda układ równań?
Mamy dwie zmienne $x$ i $y$
klamra łącząca
ze sobą równania

$ \left\{ \begin{array}{l} 2x+y=8&\\ 3x-2y=5 \end{array} \right.$
Przykład 2. I sposób - Metoda podstawiania
Wyznaczamy z dowolnego równania dowolną niewiadomą. W tym przykładzie wyznaczamy $y$ z pierwszego równania
$ \renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}} \left\{ \begin{array}{l} 2\fbox{$x$}+y=8&\\ \renewcommand\fbox{\fcolorbox{#ba302d}{#F7F8F7}} 3x-2\fbox{$y$}=5 \end{array} \right.$
Podstawiamy nasze $y$ z 1. równania w miejsce $y$ w 2. równaniu. To jest właśnie podstawienie!
$ \renewcommand\fbox{\fcolorbox{#ba302d}{#F7F8F7}} \left\{ \begin{array}{l} \fbox{$y$}=8-2x&\\ \renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}} 3\fbox{$x$}-\renewcommand\fbox{\fcolorbox{#ba302d}{#F7F8F7}}2\cdot\fbox{$(8-2x)$}=5 \end{array} \right.$
Wymnażamy nawiasy i porządkujemy równanie
$ \renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}} \left\{ \begin{array}{l} y=8-2x&\\ 3\fbox{$x$}-16+4x=5 \end{array} \right.$
Upraszczamy drugie równanie - niewiadome na lewo i liczby na prawo - pamiętając o zmianie znaku
$ \renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}} \left\{ \begin{array}{l} y=8-2x&\\ 7\fbox{$x$}=5+16 \end{array} \right.$
Przy $x$ przeszkadza nam $7$ - chcemy je usunąć. Dzielimy obustronnie przez $7$
$ \renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}} \left\{ \begin{array}{l} y=8-2x&\\ 7\fbox{$x$}=21 \end{array} \right.$
$x=3$, idziemy do równania 1 i pod x podstawiamy otrzymaną $3$
$ \renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}} \left\{ \begin{array}{l} \fbox{$x$}=21\div7=3&\\ y=8-2\cdot\fbox{$3$}=2 \end{array} \right.$
Nasze rozwiązania układu równań zapisujemy w klamrze. Warto zrobić tutaj też sprawdzenie jak w rozdziale “Równania liniowe”.
$ \left\{ \begin{array}{l} x=3&\\ y=2 \end{array} \right.$

Studencki Tip od Nati
Końcowe rozwiązania układu zapisujemy w klamrze i w kolejności alfabetycznej.

Studencki Tip od Oli
Najłatwiej znaleźć przeciwne współczynniki tam, gdzie jest sam x lub y. Wtedy wystarczy raz pomnożyć równanie przez szukany współczynnik (np. 2) i gotowe! Otrzymujemy 2x lub 2y.
Przykład 3. II sposób - Metoda przeciwnych współczynników
Teraz skupiamy się, aby przy wybranej niewiadomej stała ta sama liczba w obu równaniach, ale z przeciwnymi znakami
$ \renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}} \left\{ \begin{array}{l} 2\fbox{$x$}+y=8&\\ \renewcommand\fbox{\fcolorbox{#ba302d}{#F7F8F7}} 3x-2\fbox{$y$}=5 \end{array} \right.$
U nas najłatwiej będzie otrzymać to przy $y$. Mnożymy obustronnie pierwsze równanie przez $2$, dzięki czemu otrzymamy $+2y$. W drugim równaniu mamy $-2y$
$ \renewcommand\fbox{\fcolorbox{#ba302d}{#F7F8F7}} \left\{ \begin{array}{l} 2x+\fbox{$y$}=8 \ / \cdot2&\\ 3x-2\fbox{$y$}=5 \end{array} \right.$
Przy y stoją te same liczby (2), ale z przeciwnymi znakami - to co chcemy
$\color{red}!\ \color{black}2y-2y=\color{red}0\ !$
Dodajemy oba równania do siebie - tak jak dodajemy pisemnie,. Nic się tu nie zmienia
$ \require{cancel} \frac { + \left\{\begin{matrix} 4x+\color{red}\cancel{\color{black}2y}\color{black}=16\\ 3x-\color{red}\cancel{\color{black}2y}\color{black}=5\\ \end{matrix}\right.} {4x+3x=16+5} $
$x=3$, idziemy do pierwszego równania i pod $x$ podstawiamy otrzymane $3$
$$7x=21$$ $ \renewcommand\fbox{\fcolorbox{#8dcaae}{#F7F8F7}} \fbox{$x$}=3 $
Obliczamy wartość $y$
$$2\cdot\fbox{$3$}+y=8$$ $$6+y=8$$ $$y=2$$
Nasze rozwiązania układu równań zapisujemy w klamrze. Warto zrobić tutaj też sprawdzenie jak w rozdziale “Równania liniowe”.
$ \left\{ \begin{array}{l} x=3&\\ y=2 \end{array} \right.$
Przykład 4. III sposób - Metoda graficzna
Rysujemy funkcje liniowe z równania 1 i 2. Jak rysować funkcje i czym one są dowiesz się w następnym dziale!
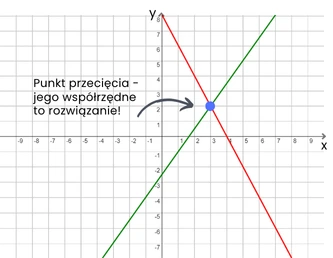
$ \left\{ \begin{array}{l} 2x+y=8&\\ 3x-2y=5 \end{array} \right.$
Wyznaczamy $y$ w obu równaniach - to właśnie wzory naszych funkcji, które będziemy rysować
