Instagram Linkedin Youtube Envelope

TU wspieramy Cię w marzeniach!

Wesprzyj

Prosta, półprosta, odcinek

Prosta

linia bez początku i końca

Półprosta

linia, która ma początek, ale nie ma końca

Odcinek

ma początek i koniec

Proste równoległe

dwie proste, które nigdy się nie przecinają

Proste prostopadłe

dwie proste, które przecinają się pod kątem prostym (90°)

Planimetria 794x794 (1)

kąty

Kąt ostry

<90°

Kąt prosty

=90°

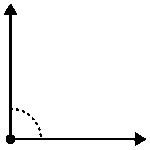
Kąt rozwarty

>90° i <180°

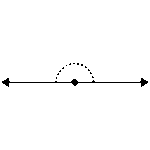
Kąt ostry

<90°

Kąt prosty

=90°

Kąt wierzchołkowy

  • dwa kąty ze wspólnym wierzchołkiem
  • kąty naprzeciw siebie są równe

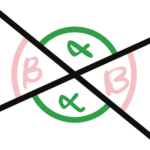
Kąt przylegający

  • ich suma to 180°
  • dwa kąty mające wspólne ramię

Kąty odpowiadające

  • proste są równoległe i kolejna prosta je przecina
  • leżą po tej samej stronie przecinającej prostej

Planimetria 794x794 (12)

Dwusieczna

  • linia dzieląca dowolny kąt w połowie (na dwie równe części)

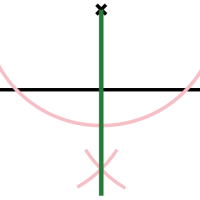
Symetralna

  • prosta dzieli odcinek na pół (na dwie równe części)
  • ta prosta jest prostopadła do odcinka

Planimetria 794x794 (14)

Środkowa

  • odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku.
  • ta prosta jes prostopadła do tego przeciwległego boku

kąty w trójkącie

Suma kątów wewnętrznych w trójkącie zawsze jest równa 180 stopni. Trójkąt może mieć tylko jeden kąt rozwarty i tylko jeden kąt prosty.

trójkąty i ich rodzaje

Trójkąty możemy podzielić na przykład ze względu na miary kątów:

Trójkąt ostrokątny

Trójkąt rozwartokątny

Trójkąt prostokątny

Oprócz tego możemy wyróżnić dwa szczególne rodzaje trójkątów:

Trójkąt równoboczny:

  • wszystkie boki tego trójkąta są równej długości.
  • wszystkie jego kąty mają po 60°

Trójkąt równoramienny:

  • dwa boki trójkąta są tej samej długości
  • dwa kąty tego trójkąta mają taką samą wartość

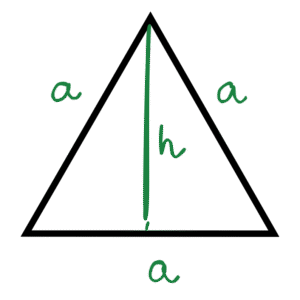
własności trójkąta równobocznego

Jako że trójkąt równoboczny ma wszystkie boki tej samej długości (i każdy kąt równy jest 60 stopni), posiada także pewne charakterystyczne właściwości.

  • linia dzieląca dowolny kąt w połowie (na dwie równe części)

$ h = \frac{a \sqrt{3}}{2} $

  • linia dzieląca dowolny kąt w połowie (na dwie równe części)

$ h = \frac{a^2 \sqrt{3}}{4} $

Przykład 1.

Dany jest trójkąt, którego wszystkie boki mają po 4 cm. Oblicz jego pole

Sposób 1

1. Obliczamy wysokość trójkąta \[a=4 h=\frac{a\sqrt{3}{2}\] \[h=2\sqrt{3}\] 2. Wykorzystujemy wzór na pole trójkąta \[P=\frac{1}{2} \cdot a \cdot h\] \[P=\frac{1}{2} \cdot 4 \cdot 2\sqrt{3} => P=4\sqrt{3}\]

Sposób 2

Obliczamy pole trójkąt z nowo poznanego wzoru na pole trójkąta równobocznego, gdzie długość boku bez potrzeby wyliczania wysokości starcza
$$P = \frac{a^2\sqrt{3}}{4} $$ 1. Wiemy, że nasz bok ma 4 cm, czyli $$a = 4$$ 2. Podstawiamy więc pod wzór: $$P = \frac{4^2\sqrt{3}}{4} => P=4\sqrt{3}$$

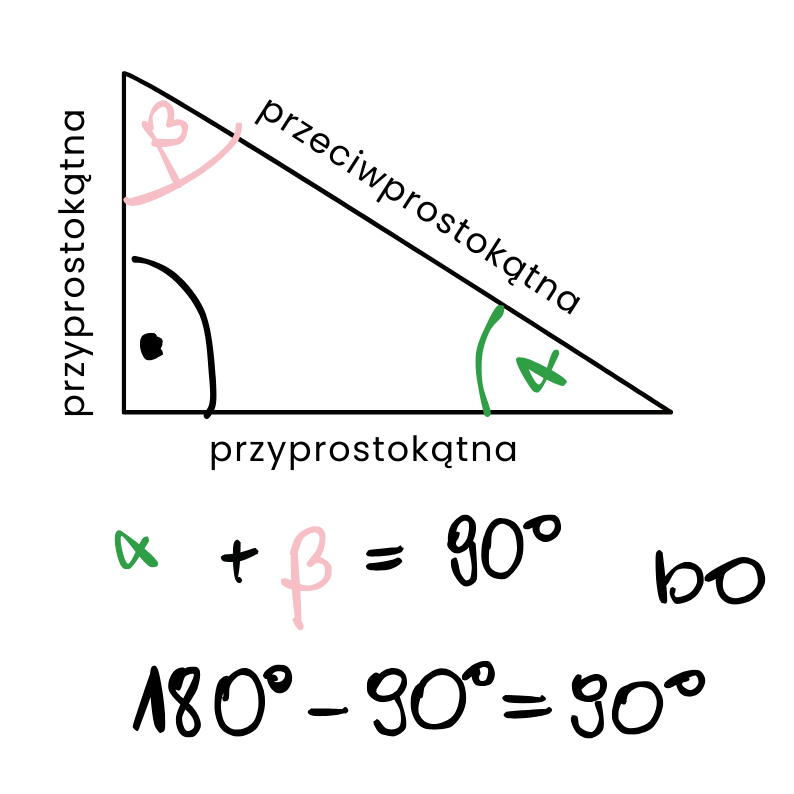
własności trójkąta prostokątnego

Z trójkątem prostokątnym zapoznaliśmy się blisko w dziale Trygonometria. Teraz jednak zwróćmy uwagę na najważniejszej właściwości tego trójkąta.

  • Suma kątów ostrych jest równa 90°
  • Do obliczenia brakującego boku możemy wykorzystać Twierdzenie Pitagorasa:

$a^2 + b^2 = c^2$

Przykład 2.

Oblicz miarę trzeciego boku trójkąta wiedząc, że przyprostokątne są równe i mają 5 cm.

Jeśli:
  1. Trójkąt jest prostokątny
  2. Masz obliczyć długość trzeciego brakującego boku
Wiedz, że kroi się Pitagoras! $$5^2 + 5^2 = c^2$$ $$50 = c^2 $$ $$ c = 5\sqrt{2}$$

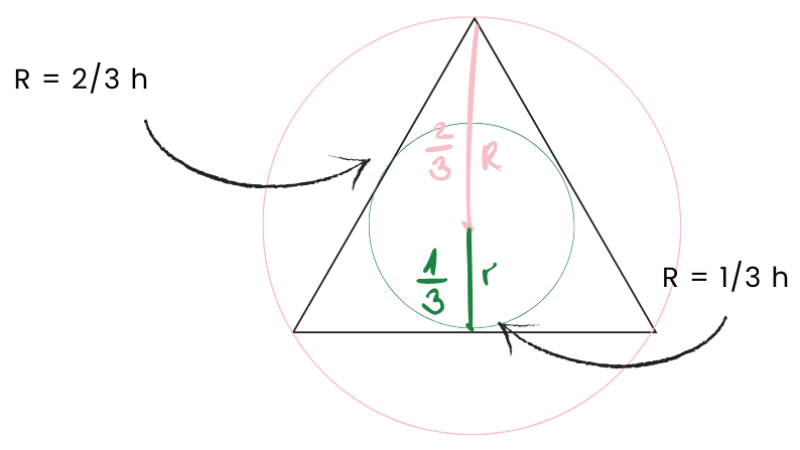
trójkąt równoboczny wpisany w okrąg oraz opisany na trójkącie

Planimetria 794x794 (22)

podobieństwo trójkątów

Trójkąty podobne to trójkąty, które mają takie same kąty, ale różnią się wielkością. Oznacza to, że ich odpowiednie boki są proporcjonalne, czyli stosunki długości odpowiadających sobie boków są równe.

Dwa trójkąty są podobne, jeśli spełniają jeden z poniższych warunków:

KK: (Kąt - Kąt) Dwa kąty jednego trójkąta są równe dwóm kątom drugiego trójkąta.

BBB: (Bok- Bok - Bok) Stosunki długości wszystkich trzech odpowiednich boków są równe.

Planimetria 794x794 (25)

BKB: (Bok- Kąt - Bok) Stosunki dwóch odpowiednich boków są równe, a kąty między tymi bokami są takie same.

Planimetria 794x794 (26)

trójkąty przystające

Trójkąty są przystające, jeśli mają identyczny kształt i rozmiar, czyli odpowiadające sobie boki są równe oraz odpowiadające sobie kąty są równe.

Aby sprawdzić, czy trójkąty są przystające, wystarczy spełnić jeden z następujących warunków:

BBB: (Bok- Bok - Bok) Wszystkie trzy boki jednego trójkąta są równe trzem bokom drugiego trójkąta.

Planimetria 794x794 (29)

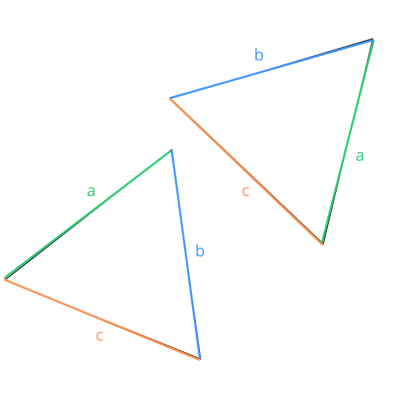
BKB: (Bok- Kąt - Bok) Dwa boki i kąt między nimi w jednym trójkącie są równe odpowiednim elementom w drugim trójkącie.

Planimetria 794x794 (27)

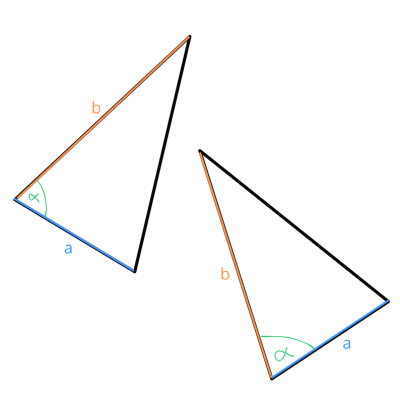
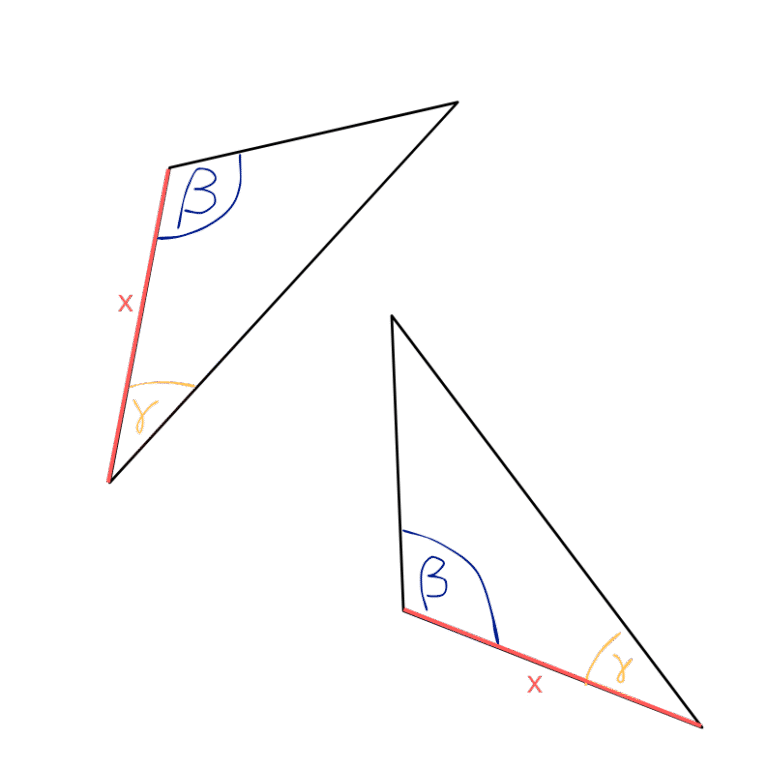
KBK: (Kąt - Bok - Kąt) Dwa kąty i bok między nimi w jednym trójkącie są równe odpowiednim elementom w drugim trójkącie.

twierdzenie o dwusiecznej kąta

Twierdzenie o dwusiecznej kąta w trójkącie mówi, że:
Dwusieczna kąta w trójkącie dzieli przeciwległy bok na odcinki proporcjonalne do długości dwóch pozostałych boków.

Jeśli w trójkącie ABC, dwusieczna kąta C przecina bok AB w punkcie D, to: $$\frac{|AD|}{|BD|} = \frac{|AC|}{|BC|}$$
  • Odcinek AD jest proporcjonalny do boku AC
  • Odcinek BD jest proporcjonalny do boku BC

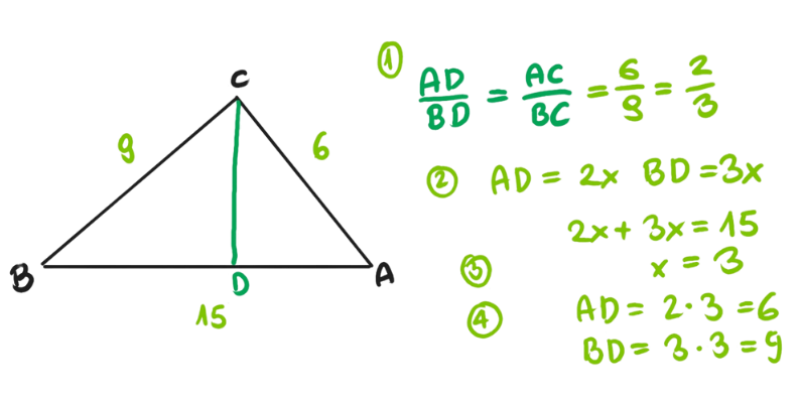
Przykład 3.

W trójkącie ABC Bok AB=6, AC=9, Dwusieczna kąta C przecina bok AB w punkcie D. Długość BC=10. Chcemy znaleźć długości odcinków BD i DC

Planimetria 794x794 (30)

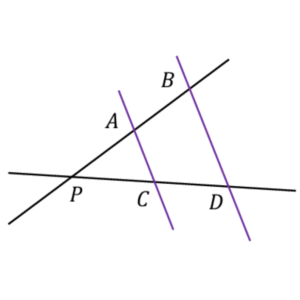
twierdzenie talesa

Twierdzenie Talesa mówi, że:
Jeśli ramiona kąta są przecięte przez dwie równoległe proste, to odcinki wyznaczone na jednym ramieniu są proporcjonalne do odpowiadających im odcinków na drugim ramieniu.

Jeśli w trójkącie ABC, dwusieczna kąta C przecina bok AB w punkcie D, to: $$\frac{|AB|}{|PA|} = \frac{|CD|}{|PC|}$$
  • Odcinek PA i PC są proporcjonalne
  • Odcinek AB i CD są proporcjonalne

Podstawowe czworokąty

Czworokąty można podzielić na różne typy, w zależności od długości boków, miar kątów czy symetrii. Najbardziej znane rodzaje czworokątów to kwadrat, prostokąt, romb, równoległobok, trapez i deltoid. Każdy z tych typów ma unikalne właściwości. Suma kątów w czworokącie wynosi zawsze 360 stopni.

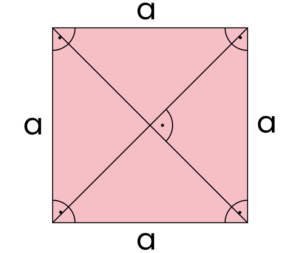
Kwadrat

  • wszystkie boki są takiej samej długości
  • każdy kąt ma 90 stopni
  • przekątne są równe
  • przekątne przecinają się pod kątem prostym (prostopadłe)
  • POLE= a * a

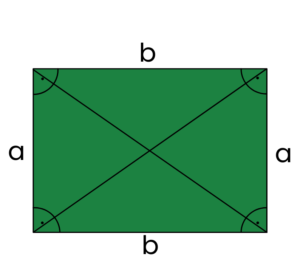
Prostokąt

  • przeciwległe boki są takiej samej długości
  • każdy kąt ma 90 stopni
  • przekątne są równe, ale nie są prostopadłe
  • POLE = a * b

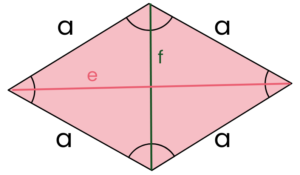
Romb

  • wszystkie boki są takiej samej długości
  • kąty na przeciwko są sobie równe
  • przekątne przecinają się pod kątem prostym (prostopadłe)
  • przekątne przecinają się w połowie
  • POLE = (e * f) / 2

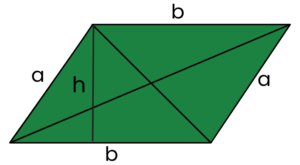
Równoległobok

  • przeciwległe boki są takiej samej długości i są równoległe
  • przekątne są róznej długości i nie są prostopadłe
  • POLE = a * h

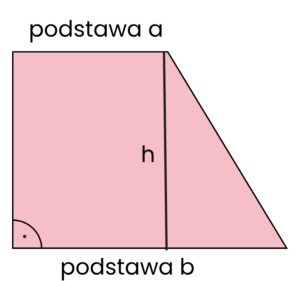
Trapez

  • jedna para boków (podstawy) jest równoległa
  • POLE = 1/2 * (a+b) * h

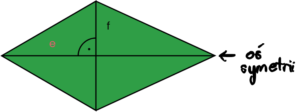
Deltoid

  • dwie pary boków są takiej samej
  • przekątne różnej długości, przecinają się pod kątem prostym
  • jedna z przekątnych jest osią symetrii
  • POLE = (e * f) / 2

Koło VS OKRĄG

Koło to figura geometryczna złożona z punktów leżących w odległości nie większej niż promień od środka. Jego podstawowe elementy to:​

Okrąg to zbiór wszystkich punktów na płaszczyźnie, które są oddalone o tę samą odległość (promień) od danego punktu (środka okręgu) albo inaczej mówiąc jest to linia, która jest zawsze tak samo daleko od jednego punktu w środku.

KOŁO

OKRĄG

Podstawowe własności Koła i Okręgu

  • Środek - punkt centralny.
  • Promień (r) - odcinek od środka do obwodu
  • Średnica (d) - odcinek przechodzący przez środek
  • Cięciwa - odcinek łączący dwa punkty leżące na okręgu
  • Obwód - długość linii otaczającej koło
  • Pole - powierzchnia wewnątrz koła

OBWÓD

$ L = 2\pi r $

Promień ma 4cm. Oblicz obwód i pole

$L = 2*\pi*4 \qquad L=8\pi$

POLE

$ P = \pi r^2 $

$P=\pi*r^2 \qquad P=16\pi$

Kąty w okręgu

Kąt wpisany (a) w okręgu to kąt, którego wierzchołek leży na okręgu, a ramiona są cięciwami okręgu.

Miara kąta wpisanego jest równa połowie miary kąta środkowego (2a), opartego na tym samym łuku.

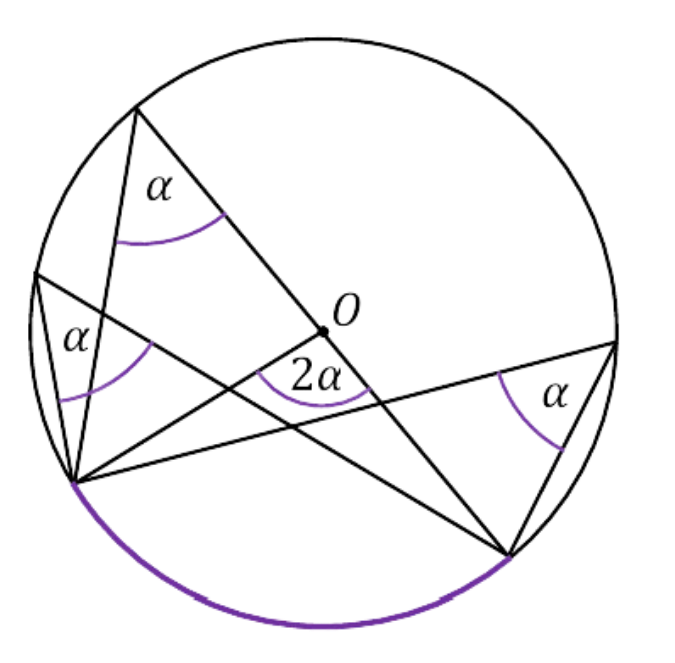
Przykład

W podanym okręgu miara kąt a wynosi 30° podaj miary kątów β i γ.

Krok 1: miara kąta β.

Zauważamy, że wszystkie trzy kąty oparte są na tym samym łuku a kat a jest kątem wpisanym, dlatego też wiemy że β jako kąt środkowy będzie dwa razy większa niż kat a czyli jego miara wynosi 60°.

Krok 2: miara kąta γ .

Analogicznie z kątem γ skoro jest oparty na tym samym łuku co a oraz także jest kątem wpisanym znaczy, że będzie miał taką samą miarę jak kąt a czyli 30°

Sieczna i styczna

Sieczna

  • prosta, która przecina okrąg w dróch punktach

Styczna

  • prosta, która ma z okręgiem dokładnie jeden punkt wspólny i jest do niego prostopadła w punkcie styczności.

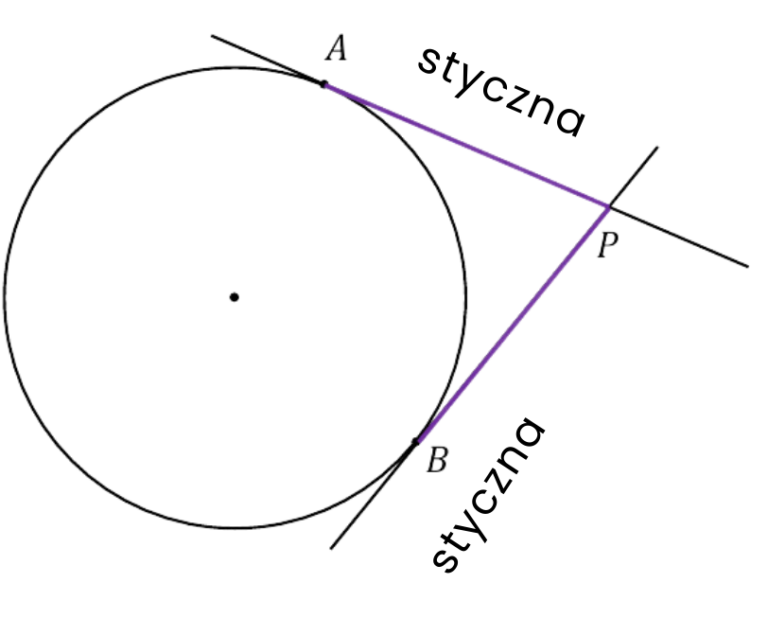
Twierdzenie o odcinkach stycznych

Jeśli A i B są styczne do okręgu i przecinają się w punkcje P to |PA| i |PB| mają taką samą długość

  • A i B to punkty styczności
  • styczne przecinają się w punkcie P
  • to odcinki |PA| = |PB|

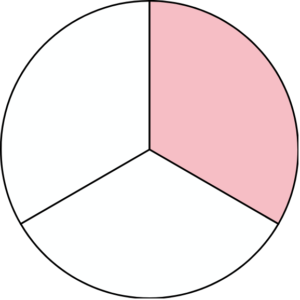
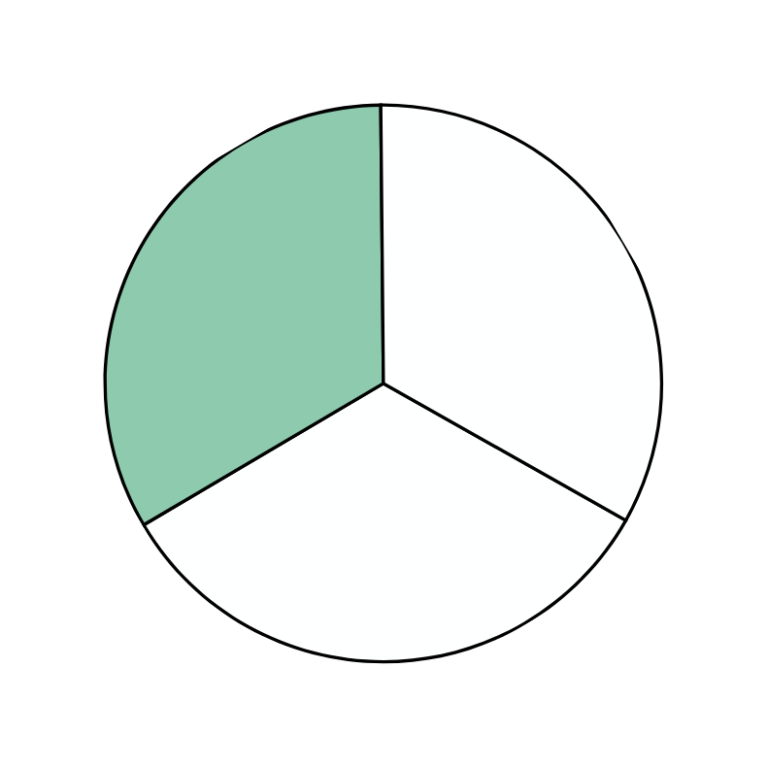
wycinek koła

Wycinek koła to fragment koła, który wygląda jak "kawałek pizzy". Jest ograniczony dwoma liniami (promieniami) wychodzącymi ze środka koła i łukiem obwodu.

Jego pole możemy obliczyć ze wzoru:

$P=\frac{\alpha}{360^\circ} \cdot \pi r^2$

A długość łuku:

$L=\frac{\alpha}{360^\circ} \cdot 2 \pi r$

Przykład

Wiedząc że długość łuku (L) jest równa 4π, promień (r) = 6. Oblicz miarę kąta a następnie oblicz pole wycinka koła.

Krok 1: miara kąta.

$4 \pi= \frac{\alpha}{360^\circ} * 2 \pi * 6$

$4 = \frac{\alpha}{360^\circ} * 12$

$\frac{4}{12}= \frac{\alpha}{360^\circ}$

$\alpha = 120^\circ$

Krok 2: Oblicz pole wycinka koła.

$P= \frac{120^\circ}{360^\circ} * \pi * 6^2$

$P= \frac{1}{3} * \pi * 36$

$P= 12 \pi$

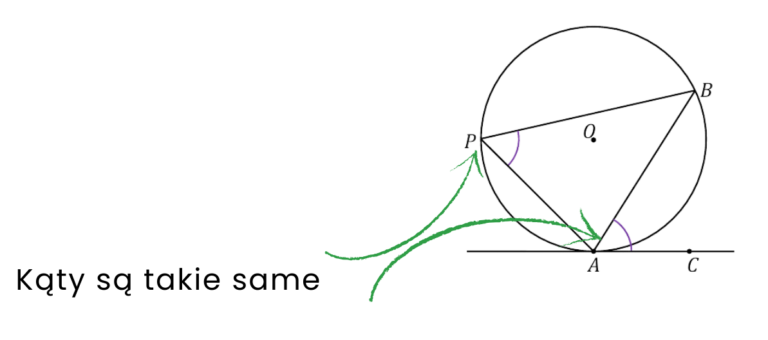
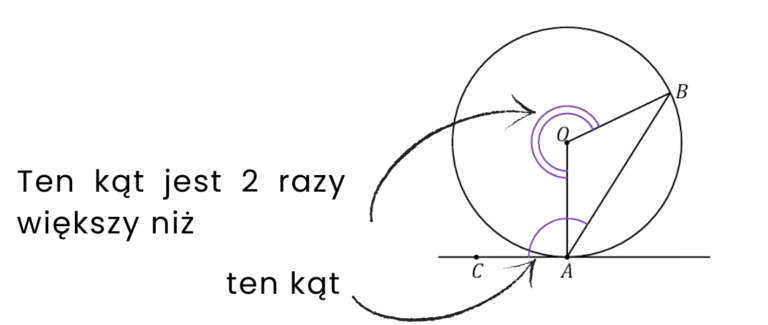
Twierdzenie o kącie między styczną i cięciwą

Kąt między styczną a cięciwą jest połową kąta środkowego, który ma ten sam łuk. Aby to zrozumieć rozważymy trzy przypadki zawarte w kartach zbiorów

Okrąg wpisany w figurę vs okrąg opisany na figurze

Bardzo często podane wyrażenia bierzemy za jednoznaczne i nie zauważamy różnicy, ta jednak występuje.

Okrąg WPISANY W trójkąt

Okrąg OPISANY NA trójkącie